Question

Please help me on this problem !

Answer 1

8.485

Explanation:

This is a right isosceles triangle, thus the angles for side a and b are going to be the same, all the angles must all add up to equal 180, thus 180 - 90 = 90 then 90 ÷ 2 = 45 so we now know that angle a and b are 45°, with that said we can now find out what the vale of x is.
Calculates 2 sides based on 3 given angles and 1 side.

a = c·sin(A)/sin(C) = 8.48528 = 6
`√(2)`

b = c·sin(B)/sin(C) = 8.48528 = 6
`√(2)`

Area =
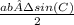`(ab·sin(C))/(2)` = 36

Perimeter p = a + b + c = 28.97056

Semiperimeter s =
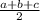`(a + b +c)/(2)` = 14.48528

Height ha =
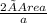`(2×Area)/(a)` = 8.48528

Height hb =
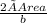`(2×Area)/(b)` = 8.48528

Height hc =
`(2×Area)/(c)` = 6

Median ma =
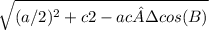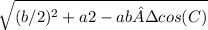`\sqrt{(a/2)^(2) + c2 - ac·cos(B)}` = 9.48683

Median mb =
`\sqrt{(b/2)^(2) + a2 - ab·cos(C)}` = 9.48683

Median mc =
`\sqrt{(c/2)^(2) + b2 - bc·cos(A)}` = 6

Inradius r =
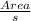`(Area)/(s)` = 2.48528

Circumradius R =
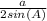`(a)/(2sin(A))` = 6