Question

PLEASE HELP!!

i'm really confused on how to do this...

(this should be 50 points but sometimes the system doesn't put that in for some reason)

I have to solve this absolute value equation: |4x-3| = |x+5|

and I have to check if there is an extraneous solution and show my work. If you can please show all your steps and explain that would be so helpful!

Answer 1

9514 1404 393

Answer:

x = {-2/5, 2 2/3}

Explanation:

There are several ways you can solve this. Maybe the simplest is to take advantage of the relation ...

`√(x^2)=|x|`

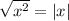
Squaring the absolute value expression on both sides gives ...

(4x -3)^2 = (x +5)^2

15x^2 -34x -16 = 0 . . . . rewrite to standard form

(5x +2)(3x -8) = 0 . . . . . factor

x = -2/5, +8/3

__

Check

To determine if one of these solutions is extraneous, we can try them both in the original equation. We find they both satisfy the equation, so neither found solution is extraneous.

For x=-2/5, |4(-2/5)-3| = |-2/5 +5| ⇒ |-4 3/5| = |4 3/5| . . . . true

For x = 8/3, |4(8/3) -3| = |8/3 +5| ⇒ |(32 -9)/3| = |(8 +15)/3| . . . . true

_____

Additional comment

Often, we solve absolute value equations using piecewise functions:

|4x -3| = {4x -3, for x ≥ 3/4; -4x +3, for x < 3/4}

|x +5| = {x +5, for x ≥ -5; -x -5, for x < -5}

Now, we have three regions in which to look for solutions: (-∞, -5], [-5, 3/4], [3/4, ∞).

In the region (-∞, -5], the equation is ...

-4x +3 = -x -5 ⇒ x = 8/3 . . . . . no solution in the region

In the region [-5, 3/4], the equation is ...

-4x +3 = x +5 ⇒ x = -2/5 . . . . . a solution in the region

In the region [3/4, ∞), the equation is ...

4x +3 = x +5 ⇒ x = 8/3 . . . . . . a solution in the region

Note that this last equation is identical to the equation for the region (-∞, -5] with both sides multiplied by -1.

Effectively, we have found the two solutions to ±(4x -3) = (x +5). The trick is to figure whether either of those solutions lies in the region for which the respective equation is defined.