Question

Please help me solve these are quadratic equations: I​

Answer 1

`\boxed {\boxed {\sf a= 3, b=7, c=2}}`

`\boxed {\boxed {\sf Y-intercept = c }}`

`\boxed {\boxed {\sf Minimum}}`

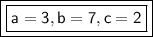
Explanation:

a. a, b, c

Quadratic equations in standard form are written as:

`f(x)= ax^2+bx+c`

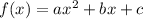
The exponents are listed from greatest to least. The quadratic is already in this form, so match up the variables and values in the equation.

`f(x)= 3x^2+7x+2`

`a=3 \\b=7 \\c=2`

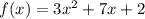
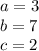
b. Y-intercept

The y-intercept for a quadratic is c.

You can also substitute 0 in for x, because the y-intercept occurs when the quadratic crosses the y-axis (at x=0).

`f(0)= 3(0)^2+7(0)+2`

`f(0)=3(0)+7(0)+2\\f(0)= 0+0+2\\f(0)=2`

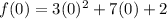
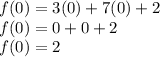
We know that c=2, so the y-intercept is c.

c. Maximum/minimum

The entire quadratic is positive, so the quadratic opens up and has a minimum.