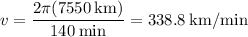Question

A satellite in circular orbit 1150 kilometers above Earth makes one complete revolution every 140 minutes. Assuming that Earth is a sphere of radius 6400 kilometers, what is the linear speed (in kilometers per minute) of the satellite? (Round your answer to one decimal place.) km/min

Answer 1

Explanation:

The radius of the orbit is r = 1150 km + 6400 km = 7550 km or

`r = 7.55×10^6\:\text{m}`

and it takes 140 minutes to complete 1 revolution. This is the same aa

`140\:\text{min}×\frac{60\:\text{s}}{1\:\text{min}} = 8400\:\text{s}`

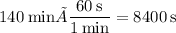
The linear speed of the satellite then is simply equal to the orbital circumference divided by the orbital period T or

`v = (2\pi r)/(T)`

`\:\;\:\:=\frac{2\pi(7.55×10^6\:\text{m})}{8.4×10^3\:\text{s}}`

`\:\:\:\:=5647.4\:\text{m/s}`

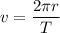
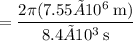
In km/min, this is

`v = \frac{2\pi(7550\:\text{km})}{140\:\text{min}} = 338.8\:\text{km/min}`