Answer:
Zeros: -1, 1, 2
Explanation:
Hi there!
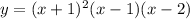
The zero-product property states that if two terms, when multiplied, equals 0, one of the terms must be equal to 0.
Therefore, we know that either (x+1), (x-1) or (x-2) is equal to 0:
x+1 = 0
x-1 = 0
x-2 = 0
Now, to solve for the zeros of the function, we can just solve for x:
x+1 = 0 ⇒ x = -1
x-1 = 0 ⇒ x = 1
x-2 = 0 ⇒ x = 2
Notice how for the function, (x+1) is raised to a power of 2. This means that the zero -1 has a multiplicity of 2.
The other zeroes, 1 and 2, have multiplicities of 1.
I hope this helps!