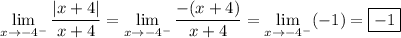I believe you're asking about the one-sided limit,
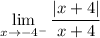
Recall the definition of absolute value:
•
 if
if
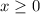
•
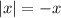 if
if
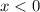
Since we're approaching -4 from the left, we're effectively focusing on a domain of
 or
or
 . So, by the definition above, we have
. So, by the definition above, we have
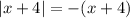 . Then in the limit, we have
. Then in the limit, we have