Question

How many moles of aluminum oxide (Al2O3) are in a sample with a mass of 204.0 g?

Answer 1

`\boxed {\boxed {\sf 2.001 \ mol \ Al_2O_3}}`

Step-by-step explanation:

We are asked to convert grams of aluminum oxide to moles. We will do this using the molar mass or mass of 1 mole of a substance. The values are found on the Periodic Table. They are equal to the atomic masses, but the units are grams per mole instead of atomic mass units.

We have the compound aluminum oxide or Al₂O₃. We must look up the molar masses of the individual elements: aluminum and oxygen.

• Al: 26.981538 g/mol
• O: 15.999 g/mol

The formula of the compound has subscripts (a subscript of 2 after Al and subscript of 3 after O). There are 2 moles of aluminum and 3 moles of oxygen in 1 mole of aluminum oxide. We must multiply the molar mass by its subscript.

• Al₂ : 26.981538 * 2=53.963076 g/mol
• O₃: 15.999 * 3=47.997 g/mol
• Al₂O₃ =53.963076 + 47.997 = 101.960076 g/mol

We convert using dimensional analysis, so we set up a ratio using the molar mass.

`\frac {101.960076 \ g \ Al_2O_3}{ 1 \ mol \ Al_2O_3}`

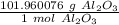
We are converting 204.0 grams to moles, so we multiply by this value.

`204.0 \ g \ Al_2O_3 *\frac {101.960076 \ g \ Al_2O_3}{ 1 \ mol \ Al_2O_3}`

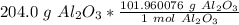
Flip the ratio so the units of grams of aluminum oxide cancel.

`204.0 \ g \ Al_2O_3 *\frac { 1 \ mol \ Al_2O_3}{101.960076 \ g \ Al_2O_3}`

`204.0 *\frac { 1 \ mol \ Al_2O_3}{101.960076}`

`\frac {204.0}{101.960076} \ mol \ Al_2O_3`

`2.00078313 \ mol \ Al_2O_3`

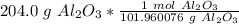
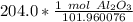
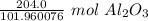
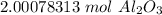
The original measurement of grams has 4 significant figures, so our answer must have the same. For the number we found, that is the thousandth place. The 7 in ten-thousandth place tells us to round the 0 up to a 1.

`2.001 \ mol \ Al_2O_3`

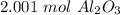
204.04 grams of aluminum oxide is equal to approximately 2.01 moles of aluminum oxide.