Question

What are the coordinates of point G ,which divides DE un the ratio 2:3?​

Answer 1

(5, 7.8)

Explanation:

There are several ways to solve this problem, but all of them involve similar triangles and ratios.

See the attached image.

The horizontal distance between points D and E is 11 - 1 = 10. If a segment 10 units long is divided in the ratio 2:3 (as shown by the two smaller segments of length a and b), then

`(a)/(b)=(2)/(3)\\(a)/(a+b)=(2)/(2+3)\\(a)/(10)=(2)/(5)`

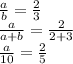
"Cross-multiply" to get

5a = 20

a = 4

To get the x-coordinate of point G, add 4 to 1, the x-coordinate of D.

The x-coordinate of G is 1 + 4 = 5.

The same idea can be used on the second coordinate of G.

The vertical distance from D to E is 15 - 3 = 12.

`(a)/(b)=(2)/(3)\\(a)/(a+b)=(2)/(2+3)\\(a)/(12)=(2)/(5)`

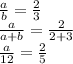
5a = 24

a = 24/5 = 4.8

The y=coordinate of G is 3 + 4.8 = 7.8