Question

Find the number of paths of length 4 between two different vertices in K5​

Answer 1

K₅ is the 5-complete graph, with adjacency matrix

`A = \begin{bmatrix} 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 & 1 \\ 1 & 1 & 0 & 1 & 1 \\ 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 \end{bmatrix}`

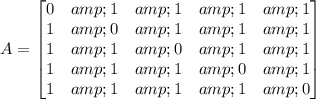
The (i, j)-th entry of the matrix A⁴ gives the number of length-4 paths from vertex i to vertex j. Computing A⁴ isn't so bad:

`A^2 =  \begin{bmatrix} 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 & 1 \\ 1 & 1 & 0 & 1 & 1 \\ 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 \end{bmatrix}  \begin{bmatrix} 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 & 1 \\ 1 & 1 & 0 & 1 & 1 \\ 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 \end{bmatrix} =  \begin{bmatrix} 4 & 3 & 3 & 3 & 3 \\ 3 & 4 & 3 & 3 & 3 \\ 3 & 3 & 4 & 3 & 3 \\ 3 & 3 & 3 & 4 & 3 \\ 3 & 3 & 3 & 3 & 4 \end{bmatrix}`

`A^4 = \begin{bmatrix} 4 & 3 & 3 & 3 & 3 \\ 3 & 4 & 3 & 3 & 3 \\ 3 & 3 & 4 & 3 & 3 \\ 3 & 3 & 3 & 4 & 3 \\ 3 & 3 & 3 & 3 & 4 \end{bmatrix} \begin{bmatrix} 4 & 3 & 3 & 3 & 3 \\ 3 & 4 & 3 & 3 & 3 \\ 3 & 3 & 4 & 3 & 3 \\ 3 & 3 & 3 & 4 & 3 \\ 3 & 3 & 3 & 3 & 4 \end{bmatrix} = \begin{bmatrix} 52 & 51 & 51 & 51 & 51 \\ 51 & 52 & 51 & 51 & 51 \\ 51 & 51 & 52 & 51 & 51 \\ 51 & 51 & 51 & 52 & 51 \\ 51 & 51 & 51 & 51 & 52 \end{bmatrix}`

We want the paths between two distinct vertices, so we ignore the entries on the diagonal and take the total of the non-diagonal entries, 20 • 51 = 1020.