Question

Let R be the region enclosed by the y-axis, the line y=1 and the curve y=x^3. A solid is generated by rotating R about the line y=1. What is the volume of the solid

Answer 1

The volume of the solid is 19.
`\overline{142857}` unit³

Explanation:

The given function is y = x³

The solid is created by revolving R about the line y = 1

We have that when y = 1, x = 1

Taking the end point as x = 2, we have the volume given by the washer method as follows;

`V = \pi \cdot \int\limits^a_b {\left( [f(x)]^2 - [g(x)]^2 \right)} \, dx`

Where;

a = 1, and b = 2, we have;

g(x) = 1

`V = \pi \cdot \int\limits^(2)_1 {\left( [x^3]^2 - [1]^2 \right)} \, dx = \pi \cdot \left[(x^7)/(7) + x \right]_1^(2) = \pi \cdot \left[(2^7)/(7) +2 -\left( (1^7)/(7) + 1\right)\right] =19(1)/(7)`

The volume of the solid, V =
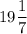`19(1)/(7)` unit³ = 19.
`\overline{142857}` unit³