Answer:
 and
and
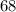 .
.
Explanation:
Let
 be the smaller one of the two number.
be the smaller one of the two number.
 must be a positive integer. The other number would be
must be a positive integer. The other number would be
 .
.
The question states that the product of the two numbers is
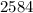 . In other words:
. In other words:
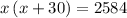 .
.
Rearrange this equation and solve for
 :
:
 .
.
The first root of this quadratic equation would be:
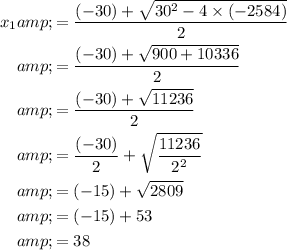 .
.
Similarly, the second root of this quadratic equation would be:
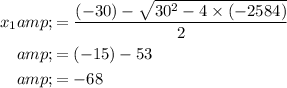 .
.
Since the question requires that both numbers should be positive,
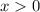 . Therefore, only
. Therefore, only
 is valid.
is valid.
Hence, the two numbers would be
 and
and
 , which is
, which is
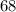 .
.