Hello there!
We are given the equation:

We are going to isolate j. First, subtract both sides by jb.
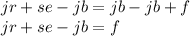
Then subtract both sides by se to leave only jr and jb.
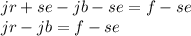
For jr-jb, we can common factor out the j-term.

For r-b, treat it as one term. Then we divide both sides by r-b.
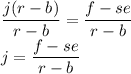
Hence, j = f - se / r - b
Alternate Solution
This is an alternate solution. We can simplify the fractional expression by separating each terms.
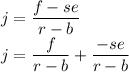
Since se is in negative, we replace + as - and cancel -se to se.
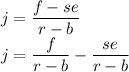
The simplifed answer is j = ( f / r - b ) - ( se / r - b l
These two answers work and are correct.
Let me know if you have any questions!
Topic: Literal Equation (Factorization Involved)