Question

A 63 foot long cable is anchored in the ground and

attached to the top of a light pole at an angle of
elevation of 52 degrees. Find the height of the light pole
to the nearest foot.

Answer 1

The height of the light pole to the nearest foot is approximately 50 feet

Explanation:

The parameters given in the question are;

The length of the cable = 63 feet

The angle of elevation of the cable to the top of the light pole = 52°

With the assumption that the light pole is perpendicular to the ground, the figure formed by the light pole, the distance of the of the cable from the base of the light pole and the length of the cable form a right triangle

The question can be answered by using trigonometric relations for the sine of the given angle as follows;

`sin ( \theta) = (Opposite \ leg \ length)/(Hypotenuse \ length)`

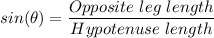
The opposite leg length of the formed right triangle = The height of the light pole

The hypotenuse length = The length of the cable = 63 feet

The angle, θ = The angle of elevation = 52°

Plugging in the values, gives;

`sin (52 ^ {\circ}) = (The \ height \ of \ the \ light \ pole )/(63 \ feet)`

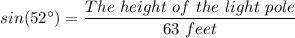
∴ The height of the light pole = 63 feet × sin(52°) ≈ 49.645 feet

The height of the light pole to the nearest foot ≈ 50 feet.