Question

Check down the image that’s give below

Answer 1

`\frac{3x}{ {x}^(2) + 6x + 9} + \frac{x + 3}{ {x}^(2) - 9 }`

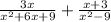
In the first fraction, we have to factorise the denominator using (a + b)² = a² + 2ab + b². And in the second fraction, we have to factorise the denominator using a² - b² = (a - b)(a + b) identity.

`= \frac{3x}{ {(x)}^(2) + 2(x)(3) + ( {3)}^(2) } + (x + 3)/((x)^(2) - (3)^(2) ) \\ = (3x)/((x + 3) ^(2) ) + (x + 3)/((x + 3)(x - 3))`

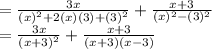
From the second fraction, cancel out from both sides (x + 3), the we get:

`= (3x)/((x + 3) ^(2) ) + (1)/((x - 3)) \\ = (3x(x - 3) + 1(x + 3) ^(2) )/((x + 3)^(2) (x - 3)) \\ = \frac{3x ^(2) - 9 x+ {x}^(2) + 6x + 9}{ {(x + 3)}^(2) (x - 3)} \\ = \frac{ {4x}^(2) - 3x + 9}{(x + 3)(x + 3)(x - 3)}`

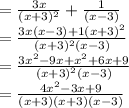
Answer:

`\frac{ {4x}^(2) - 3x + 9}{(x + 3)(x + 3)(x - 3)}`

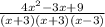
Hope you could understand.

If you have any query, feel free to ask.