Answer:
n=64
Explanation:
Let think algebracially. One of the terms in the set is a fraction. A natural number must be a whole number so this means that
n must be a multiple of 8.
*N must be a multiple of 8.
Look at the third term, we know that a square root must produce a perfect square term to get a natural number. So n must be a multiple of 8 that makes the radical a perfect square
Perfect squares are.
0,1,4,9,16,25,36,49,64,81,100,121,144,169,196,225, 256, 289
N has to compute a sum greater than 225 so the perfect squares we look at must be greater than 225.
The next one is 256 but
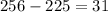
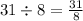
which isn't rational so 256 won't work. Let try 289
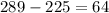
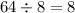
and
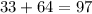
So 64 works. 64 is the answer
n=64