Question

Three of the four vertices of a rectangle are located at (4, 2), (7, 2) and (4, 8). a. What are the coordinates of the missing vertex? ( , ) b. Find the area and perimeter of the rectangle. Area = square units Perimeter = units

Answer 1

a) The coordinates of the missing vertex = (7, 8)

b) Area = 18 square units

Perimeter = 18 units

Explanation:

a) We know three of the four vertices:

A: (4, 2) C ______ D(?)

B: (7, 2) | |

C: (4, 8) A |______| B

To find the coordinates of the missing vertex we need to calculate the distance in the x-direction from point A to point B:

`B_(x) - A_(x) = 7 - 4 = 3`

Hence, the distance of point D from point C in the x-direction is:

`D_(x) = C_(x) + 3 = 4 + 3 = 7`

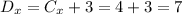
Now, to find the coordinate in "y" we need to calculate the distance in the y-direction between point C and point A:

`C_(y) - A_(y) = 8 - 2 = 6`

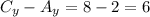
Then, the distance of point D from point B in the y-direction is:

`D_(y) = B_(y) + 6 = 2 + 6 = 8`

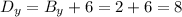
Therefore, the coordinates of the missing vertex (point D) are:

`D = (D_(x), D_(y)) = (7, 8)`

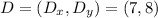
b) The area of the rectangle is:

`a = (B_(x) - A_(x))*(C_(y) - A_(y)) = 3*6 = 18 units^(2)`

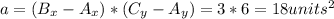
The perimeter is given by:

`p = 2*(3 + 6) = 18 units`

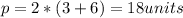
I hope it helps you!