Question

NO LINKS!! Please help fill in the blanks. Part 9a​

Answer 1

Example:

Carbon-14 has a radioactive half-life of 5,730 years. Use the radioactive decay equation to find the age of a fossil that contains 20% of its original carbon-14.

`\begin{array} \cline{1-2}& \\ \text{Substitute the known values into the} & 0.2A_0 = A_0(0.5)^{(t)/(5730)}\\\text{equation} & \\ \cline{1-2}& \\\text{Isolate the exponential expression} & 0.2 = (0.5)^{(t)/(5730)}\\ & \\ \cline{1-2} & \\\text{Rewrite into log form} & \log_(0.5)(0.2) = (t)/(5730)\\ & \\ \cline{1-2}\end{array}`

`\begin{array}c \cline{1-2}& \\ \text{Isolate the variable} & 5730\log_(0.5)(0.2) = t\\& \\ \cline{1-2}& \\ \text{Use the }\underline{\text{chan}}\text{g}\underline{\text{e}} \ \underline{\text{of}} \ \underline{\text{base}}\text{ formula to} & 5730(\log(0.2))/(\log(0.5)) = t\\ \text{rewrite the logarithmic expression and solve} & \\ \text{for t} & 13,304.64798\approx t\\ & \\ \cline{1-2}\end{array}`

The fossil is approximately 13 thousand years old.

Side note: carbon-14 decays into nitrogen-14 and a beta particle.

====================================================

Question: How long will it take $2,000 to double if it is deposited in an account with an interest rate of 5% compounded continuously?

When interest is compounded continuously, the equation
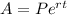`A = Pe^(rt)` represents the balance, A, after t years, where r is the rate of interest and P is the beginning balance or principal .

Twice $2,000 is $4,000. Substitute these variables into the compound interest formula, isolate the exponential expression and solve for t.

`A = Pe^(rt)\\\\4000 = 2000e^(0.05t)\\\\4000/2000 = e^(0.05t)\\\\2 = e^(0.05t)\\\\\text{Ln}(2) = \text{Ln}(e^(0.05t))\\\\\text{Ln}(2) = 0.05t\\\\(\ln(2))/(0.05) = t\\\\13.8629 \approx t`

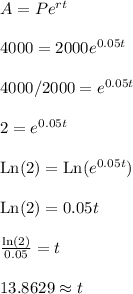
In about 13.86 years, the amount doubles.