Answer:
i = 17.6 10⁻⁶ A
Step-by-step explanation:
The charge of a capacitor in a series circuit is
i =
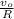
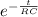 (1)
(1)
R i = V₀ e^{ - \frac{t}{RC} }
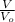 = e^{ - \frac{t}{RC} }
= e^{ - \frac{t}{RC} }
they tell us that the voltage is 80% bone
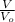 = 0.80
= 0.80
we substitute
0.80 = e^{ - \frac{t}{RC} }
ln 0.80 =
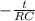
t = - RC ln 0.80
in the problem they give the value of R = 2.0 10⁶ Ω and C = 4.0 10⁻⁶ F
t = - 2 10⁶ 4 10⁻⁶ ln 0.8
t = 1,785 s
we substitute in equation 1
i =
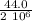

i = 22 10⁻⁶
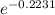
i = 17.6 10⁻⁶ A