In a logarithmic equation, the variable is in the argument of the logarithm.
As with other types of equations, the goal in solving is to isolate the variable on one side of the equation.
---------
Example: Solve
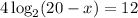 for x.
for x.

Let's check the answer.

We have rounding error. This is why we don't land exactly on 12, but we get really close.
---------
Or we could check the answer this way
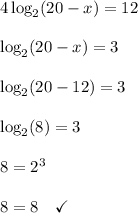
The answer is confirmed.