Answer:
See Explanation
Explanation:
Incomplete question as the function is not given. So, I will give a general solution
Required
Determine the average rate of change from t = 2 to 4
Average rate of change is :
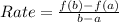
In this case: a = 2 and b = 4
So, we have:
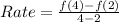
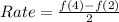
Assume that the exponential function is:
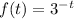
f(4) and f(2) will be:
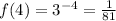
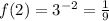
So:
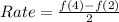
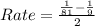
Take LCM
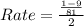
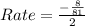
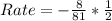
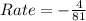
So, the average rate of change is a decrease of 4/81