Answers:
When we evaluate a logarithm, we are finding the exponent, or power x, that the base b, needs to be raised so that it equals the argument m. The power is also known as the exponent.
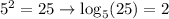
The value of b must be positive and not equal to 1
The value of m must be positive
If 0 < m < 1, then x < 0
A logarithmic equation is an equation with a variable that includes one or more logarithms.
===============================================
Step-by-step explanation:
Logarithms, or log for short, basically undo what exponents do.
When going from
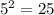 to
to
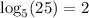 , we have isolated the exponent.
, we have isolated the exponent.
More generally, we have
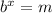 turn into
turn into
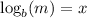
When using the change of base formula, notice how
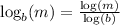
If b = 1, then log(b) = log(1) = 0, meaning we have a division by zero error. So this is why
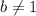
We need b > 0 as well because the domain of y = log(x) is the set of positive real numbers. So this is why m > 0 also.