Answer:
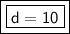
Explanation:
The distance between two points can be calculated using the following formula.

In this formula, (x₁, y₁) and (x₂, y₂) are the two points. We are given the points (-9, -2) and (-3,6). If we match the value with the corresponding variable we see that:
- x₁= -9
- y₁= -2
- x₂= -3
- y₂= 6
Substitute the values into the formula.
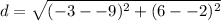
Solve inside the parentheses. Remember that 2 back to back negative signs become a plus sign.
- (-3 - -9)= (-3+9)= 6
- ( 6- -2)= (6+2) =8
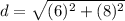
Solve the exponents. Multiply the number by itself.
- (6)²= 6*6= 36
- (8)²= 8*8= 64
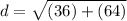
Add.
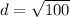
Take the square root of the number.

The distance between the points (-9, -2) and (-3, 6) is 10.