Question

On a coordinate grid, point P has coordinates (3,2). Points Q and R have coordinates (8,6) and (4,-5) respectively. Which of points Q and R is closer to point P? You must show full working to support your answer.

Answer 1

Answer: Point Q is closer

===========================================

Step-by-step explanation:

Use the distance formula to calculate the length of segment PQ

`P = (x_1,y_1) = (3,2) \text{ and }Q = (x_2,y_2) = (8,6)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((3-8)^2 + (2-6)^2)\\\\d = √((-5)^2 + (-4)^2)\\\\d = √(25 + 16)\\\\d = √(41)\\\\d \approx 6.40312\\\\`

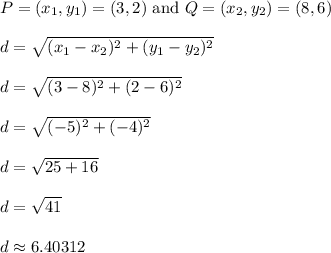
PQ is roughly 6.403 units long.

Repeat the same type of calculations, but this time we want to find the length of segment PR.

`P = (x_1,y_1) = (3,2) \text{ and }R = (x_2,y_2) = (4,-5)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((3-4)^2 + (2-(-5))^2)\\\\d = √((3-4)^2 + (2+5)^2)\\\\d = √((-1)^2 + (7)^2)\\\\d = √(1+49)\\\\d = √(50)\\\\d \approx 7.07107\\\\`

--------------------

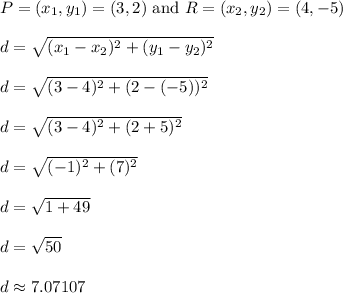
To summarize, we have these approximate segment lengths.

• PQ = 6.403
• PR = 7.071

Segment PQ is shorter, which means Q is the closer point.