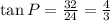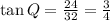Answer:
Image 1
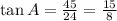
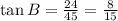
Image 2
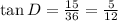
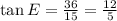
Image 3
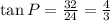
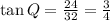
Explanation:
Trigonometrically speaking, the tangent of an angle in a right triangle is the ratio of the length opposite to the angle to the length adjacent to the angle. Then, we solve for each case:
Image 1
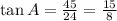
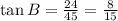
Image 2
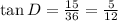
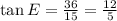
Image 3