Question

What single percentage change is equivalent to a 12% decrease followed by a 18% increase?

Answer 1

Given:

12% decrease followed by a 18% increase.

To find:

The single percentage change is equivalent to the given set of percentages.

Solution:

Let the initial value be 100.

After 12% decrease, the value is:

`v_1=100-(12)/(100)* 100`

`v_1=100-12`

`v_1=88`

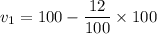
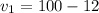
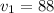
After 18% increase, the value is:

`v_2=88+(18)/(100)* 88`

`v_2=88+15.84`

`v_2=103.84`

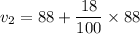
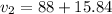
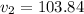
The initial value is 100 and the new value in 103.84. So, it represents increase in the value. So, increase percentage is

`Increase\%=\frac{\text{New -Initial}}{\text{Initial}}* 100`

`Increase\%=(103.84-100)/(100)* 100`

`Increase\%=3.84`

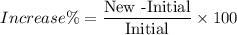
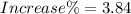
Therefore, the value increased by 3.84%.