Question

The diagram shows a 5 cm x 5 cm x 5 cm cube.

A
Calculate the length of the diagonal AB.
Give your answer correct to 1 decimal place.
5 cm
L
5 cm
B В
5 cm

Answer 1

8.7

Explanation:

hope this help!

Answer 2

~8.66cm

Explanation:

The length of a diagonal of a rectangular of sides a and b is

`√(a^2+b^2)`

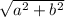
in a cube, we can start by computing the diagonal of a rectangular side/wall containing A and then the diagonal of the rectangle formed by that diagonal and the edge leading to A. If the cube has sides a, b and c, we infer that the length is:

`\sqrt{√(a^2+b^2)^2 + c^2} = √(a^2+b^2+c^2)`

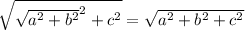
Using this reasoning, we can prove that in a n-dimensional space, the length of the longest diagonal of a hypercube of edge lengths
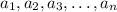`a_1, a_2, a_3, \ldots, a_n` is

`√(a_1^2 + a_2^2 + a_3^2 + \ldots + a_n^2)`

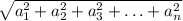
So the solution here is

`√((5cm)^2 + (5cm)^2 + (5cm)^2) = √(75cm^2) = 5√(3cm^2) \approx 5\cdot 1.732cm = 8.66cm`