Given:
A figure of a circle and two secants on the circle from the outside of the circle.
To find:
The measure of angle KLM.
Solution:
According to the intersecting secant theorem, if two secant of a circle intersect each other outside the circle, then the angle formed on the intersection is half of the difference between the intercepted arcs.
Using intersecting secant theorem, we get
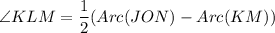
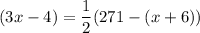
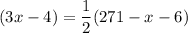
Multiply both sides by 2.
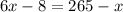
Isolate the variable x.
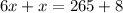
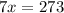
Divide both sides by 7.
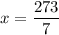
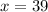
Now,
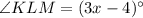
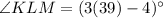
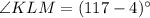
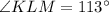
Therefore, the measure of angle KLM is 113 degrees.