Answer:
$15,000 was invested at 7%
$3,000 was invested at 8%
Explanation:
Let
 be the amount of money you spend on the 7% account and
be the amount of money you spend on the 7% account and
 be the amount of money you spend on the 8% account. With the information given, you can set up two equations:
be the amount of money you spend on the 8% account. With the information given, you can set up two equations:
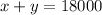
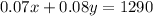
Rearrange the first equation and multiply the second equation to get:
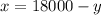
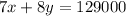
Then, substitute
 for
for
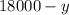 in the second equation to get:
in the second equation to get:
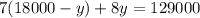
Use the distributive property (
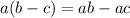 ) to get:
) to get:
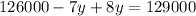
Subtract
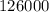 from both sides and combine like terms to get:
from both sides and combine like terms to get:
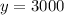
Thus, substitute
 for
for
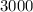 in the first original equation to get:
in the first original equation to get:
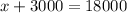
Finally, subtract
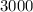 from both sides to reach:
from both sides to reach:
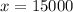
Our answer is $15,000 was invested at 7% and $3,000 was invested at 8%.
Hope this helps :)