Question

Factor completely .
4u^2 - 100

Answer 1

`4\, (u + 5)\, (u - 5)`.

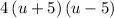Explanation:

Make use of the fact that the difference of two perfect squares,
`(x^(2) - y^(2))`, could be rewritten as a product of the form
`(x + y)\, (x - y)`. That is:

`x^(2) - y^(2) = (x + y)\, (x - y)`.

In this question, the two squares are
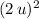`(2\, u)^(2)` and
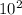`10^(2)`, respectively. Thus:

`\begin{aligned}& 4\, u^(2) - 100 \\=\; & (2\, u)^(2) - (10)^(2) \\ =\; & (2\, u + 10) \, (2\, u - 10) \end{aligned}`.

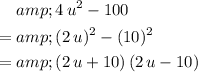Simplify this expression even further:

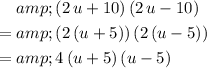`\begin{aligned} & (2\, u + 10) \, (2\, u - 10) \\ =\; & (2\, (u + 5))\, (2\, (u - 5)) \\ =\; & 4\, (u + 5)\, (u - 5)\end{aligned}`.

Answer 2

4(u - 5)(u + 5)

Explanation:

We have the expression,
`4u^2-100`

Factor out 4:
`4(u^2-25)`

25 can be written as
`5^2`

Use difference of squares property:
`a^2-b^2=(a-b)(a+b)`

`4(u^2-5^2)`

=
`4(u-5)(u+5)`