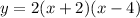Question

The graph of a quadratic relation has zeros at -2 and 4 and passes through the point (1,-18). Determine the equation of the parabola in factored form.

Answer 1

y=2(x+2)(x-4)

Explanation:

Factored form of a quadratic relation: y = (x - a)(x - b), where a and b are zeroes.

We are given the zeroes, which are -2 and 4. We can write the quadratic equation as:

`y=(x - (-2))(x - 4)\\y=(x+2)(x-4)`

Let's check if the equation passes through the point (1, -18).

`y=(1+2)(1-4)\\y=3*(-3)\\y=-9`

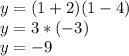
Hmm nope. So we must modify the equation somehow to satisfy the problem.

Vertically or horizontally changing the equation won't do because this would change every point, including the zeroes, which we don't want to. Maybe we can scale it, so we either multiply or divide the equation.

When we plugged in 1, we got -9, which is exactly half to -18. We can try to double the equation.

By multiplying it by 2, we get:

`y=2(x+2)(x-4)`

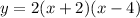
Okay, let's check this once again!

`y=2(1+2)(1-4)\\\\y=2(3)(-3)\\y=2(-9)\\y=-18`

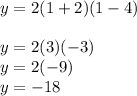
Hey! This works! We were able to plug in 1 and get -18 while maintaining the zeroes!

So, the equation that satisfies the problem is:

`y=2(x+2)(x-4)`