Given:
The measure of three sides of a triangle are 8, 7 and 14.
To find:
The measure of the angle opposite the side of length 8.
Solution:
According to the Law of Cosine:
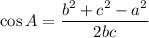
Let a=8, b=7 and c=14, then by using Law of Cosine, we get
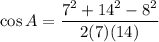
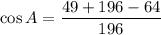
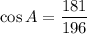
Taking cos inverse on both sides.

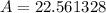

Therefore, the measure of the angle opposite the side of length 8 is 22.6 degrees.