Question

. A triangle has side lengths of 8, 7, and 14. To the nearest tenth of a degree find the measure of the angle opposite the side of length 8.

Answer 1

Given:

The measure of three sides of a triangle are 8, 7 and 14.

To find:

The measure of the angle opposite the side of length 8.

Solution:

According to the Law of Cosine:

`\cos A=(b^2+c^2-a^2)/(2bc)`

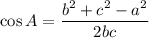
Let a=8, b=7 and c=14, then by using Law of Cosine, we get

`\cos A=(7^2+14^2-8^2)/(2(7)(14))`

`\cos A=(49+196-64)/(196)`

`\cos A=(181)/(196)`

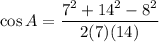
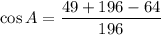
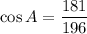
Taking cos inverse on both sides.

`A=\cos^(-1)(181)/(196)`

`A=22.561328`

`A\approx 22.6`

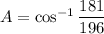
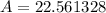
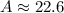
Therefore, the measure of the angle opposite the side of length 8 is 22.6 degrees.