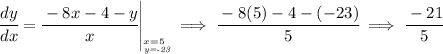Question

CALC BC HELPPP!!!??? 100PTS!!!

4x2+4x+xy=5 and y(5)=−23, find y′(5) by implicit differentiation.

Answer 1

the assumption being that "x" is a plain variable whilst "y" is a function, that matters because the chain rule would be needed for a function, not so for a plain variable.

`4x^2+4x+xy=5\implies 8x+4+\stackrel{\textit{product rule}}{\left( 1\cdot y+x\cdot \cfrac{dy}{dx} \right)}=0 \\\\\\ x\cfrac{dy}{dx}=-8x-4-y\implies \cfrac{dy}{dx}=\cfrac{-8x-4-y}{x}`

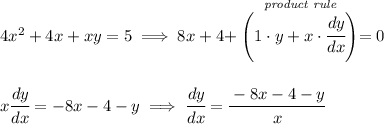
now, we know that y(5) = -23, which is another way of saying that when x = 5, y = -23, but we already knew that, we can get that by simply plugging it into the equation hmmm y'(5), well

`\left. \cfrac{dy}{dx}=\cfrac{-8x-4-y}{x} \right|_{\stackrel{x=5~}{\textit{\tiny y=-23}}}\implies \cfrac{-8(5)-4-(-23)}{5}\implies \cfrac{-21}{5}`

Answer 2

`(dy)/(dx)=-(21)/(5)`

Explanation:

Given function:

`4x^2+4x+xy=5`

To differentiate the given function using implicit differentiation:

`(d)/(dx)4x^2+(d)/(dx)4x+(d)/(dx)xy=(d)/(dx)5`

Differentiate terms in x only (and constant terms) with respect to x:

`\implies 8x+4+(d)/(dx)xy=0`

Use the product rule to differentiate the term in x and y:

`\textsf{let }\: u = x \implies (du)/(dx) = 1`

`\textsf{let }\: v = y \implies (dv)/(dx) = (dy)/(dx)`

`\begin{aligned}\implies (dy)/(dx) & =u (dv)/(dx)+v(du)/(dx)\\ & =x(dy)/(dx)+y\end{aligned}`

`\implies 8x+4+x(dy)/(dx)+y=0`

Rearrange to make dy/dx the subject:

`\implies x(dy)/(dx)=-8x-y-4`

`\implies (dy)/(dx)=-(8x+y+4)/(x)`

When x = 5, y = -23. Therefore, substitute these values into the differentiated function to find y'(5):

`\implies (dy)/(dx)=-(8(5)+(-23)+4)/(5)`

`\implies (dy)/(dx)=-(21)/(5)`