Question

Using algebra, find the point at which the line k(x)=4x+12 intersects the line f(x)=1x+3

Answer 1

(-3, 0)

Explanation:

We are given two linear functions:

`k(x)=4x+12\text{ and } f(x)=x+3`

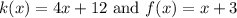
And we want to find the point at which the two lines intersect.

At the point the two lines intersect, their y-values will be the same. In other words, we can set their functions equal to each other and solve for x. Thus:

`k(x)=f(x)`

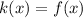
Substitute:

`4x+12=x+3`

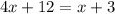
Solve for x. Subtracting x from both sides yields:

`3x+12=3`

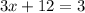
And subtracting 12 from both sides yields:

`3x=-9`

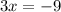
Thus, the x-coordinate of the point where the two lines intersect is:

`x=-3`

To find the y-value, we can use either function. Using the second function, we acquire:

`f(-3)=(-3)+3=0`

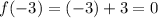
(You will obtain the same result if you use the first function. Try it!)

Thus, the point of intersection is (-3, 0).