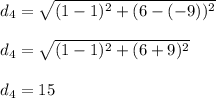Question

Find the distance between each pair of points. You may want to plot the points. (2 pts each) (2, 3), (7, 3) (-2, 5), (-2, -3) (-8, 5), (-2, 5) (-9, 1), (6, 1)

Answer 1

(1) First pair; (2, 3), (7, 3), d₁ = 5

(2) Second pair; (-2, 5), (-2, -3), d₂ = 8

(3) Third pair; (-8, 5), (-2, 5), d₃ = 6

(4) Fourth pair; (-9, 1), (6, 1), d₄ = 15

Explanation:

Given pair of points;

(1) (2, 3), (7, 3)

(2) (-2, 5), (-2, -3)

(3) (-8, 5), (-2, 5)

(4) ) (-9, 1), (6, 1)

The distance between each pair of points is calculated as follows;

`d = √((y_2-y_1)^2 + (x_2-x_1)^2)`

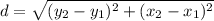
(1) first pair; (2, 3), (7, 3)

`d_1 = √((3-3)^2 + (7-2)^2) \\\\d_1 = 5`

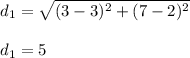
(2) second pair; (-2, 5), (-2, -3)

`d_2 = √((-3-5)^2 + (-2-(-2))^2)\\\\d_2 = √((-3-5)^2 + (-2+2)^2) \\\\d_2 = 8`

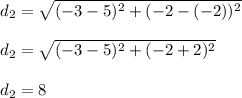
(3) Third pair; (-8, 5), (-2, 5)

`d_3 = √((5-5)^2 + (-2-(-8))^2)\\\\d_3 = √((5-5)^2 + (-2+8)^2) \\\\d_3 = 6`

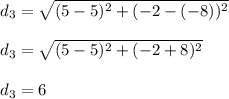
(4) Fourth pair; (-9, 1), (6, 1)

`d_4 = √((1-1)^2 + (6-(-9))^2)\\\\d_4 = √((1-1)^2 + (6+9)^2) \\\\d_4 = 15`