Given:
The equation are
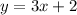
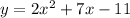
To find:
The coordinates of intersection points.
Solution:
We have,
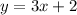 ...(i)
...(i)
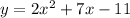 ...(ii)
...(ii)
From (i) and (ii), we get
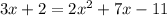

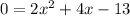
If a quadratic equation is
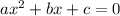 , then by quadratic formula:
, then by quadratic formula:

In the equation
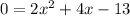 , we have
, we have
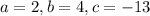 .
.
Using quadratic formula, we get


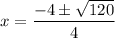
Now,
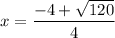 and
and
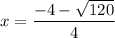
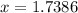 and
and
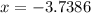
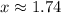 and
and
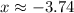
Putting x=1.74 in (i), we get
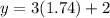
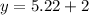
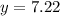
Putting x=-3.74 in (i), we get
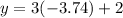
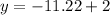
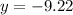
Therefore, the coordinates of the intersection points are (1.74, 7.22) and (-3.74,-9.22).