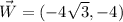Answer:
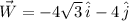 ,
,
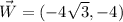
Explanation:
If
 is in standard position, then its direction is counterclockwise with respect to
is in standard position, then its direction is counterclockwise with respect to
 semiaxis. A vector is defined by its magnitude and direction, that is:
semiaxis. A vector is defined by its magnitude and direction, that is:
 (1)
(1)
Where:
 - Magnitude, no unit.
- Magnitude, no unit.
 - Direction, measured in sexagesimal degrees.
- Direction, measured in sexagesimal degrees.
If we know that
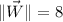 and
and
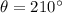 , then the resulting vector is:
, then the resulting vector is:
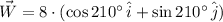
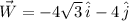
Which is also equivalent to: