Question

Please help solve this question been stuck for a while​

Answer 1

7.7

Explanation:

To find the intersection points of the line and the circle we have to set up a system with their equations and solve. The system would look like this:

`\left \{ {{x=1 } \atop {x^2+y^2=16}} \right.`

To solve, substitute 1 for x in the second equation to get:

`1^2+y^2=16`

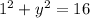
Solving, we get:

`y=√(15), y=-√(15)`

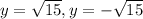
Therefore, the two points of intersection are
`(1,√(15) )` and
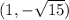`(1,-√(15))`. The distance between these two points (the length of the chord in the circle) is
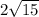`2√(15)` which is 7.745966692414... which is 7.7 rounded to the nearest tenth.

Hope this helps :)