Question

An electron travels at 2.0 x 107 m/s in a plane perpendicular to a 0.1 T magnetic field. What is the radius and period of the electron? (hint: recall centripetal force and tangential velocity)

Answer 1

r = 0.001137 m = 1.137 mm

T = 3.57 x 10⁻¹⁰ s

Step-by-step explanation:

In order for the electron to remain in a fixed circle centripetal force must be equal to the magnetic force:

`Centripetal\ Force = Magnetic\ Force\\(mv^2)/(r) = qvB\ Sin\theta\\\\r = (mv^2)/(qvB\ Sin\theta) = (mv)/(qB\ Sin\theta)`

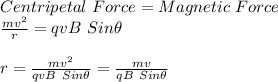
where,

r = radius = ?

m = mass of electron = 9.1 x 10⁻³¹ kg

v = speed of electron = 2 x 10⁷ m/s

q = charge on electron= 1.6 x 10⁻¹⁹ C

B = Magnetic Fild Strength = 0.1 T

θ = Angle between velocity and magnetic field = 90° (perpendicular)

`r = ((9.1\ x\ 10^(-31)\ kg)(2\ x\ 10^7\ m/s))/((1.6\ x\ 10^(-19)\ C)(0.1\ T)Sin90^o)\\\\`

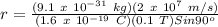
r = 0.001137 m = 1.137 mm

Now, for the period of the electron:

`v = (2\pi r)/(T)\\\\T = (2\pi r)/(v)\\`

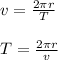
where,

T = Time period required o cover a distance equal to cirumference = ?

`T = (2\pi(0.001137\ m))/(2\ x\ 10^7\ m/s)\\\\`

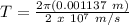
T = 3.57 x 10⁻¹⁰ s