Question

A spinner has 25 congruent sections. There are 12 orange, 4 red, 6 blue, and 3 purple sections on the spinner. Which decimal represents the probability that the first spin will stop on a blue section?

Answer 1

Given:

Total number of congruent sections = 25

Orange sections = 12

Red sections = 4

Blue sections = 6

Purple sections = 3

To find:

The probability that the first spin will stop on a blue section.

Solution:

The probability that the first spin will stop on a blue section is the fraction of number of blue sections and total number of sections.

`P=\frac{\text{Number of blue sections}}{\text{Total number of sections}}`

`P=(6)/(25)`

`P=0.24`

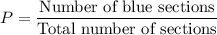
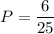
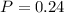
Therefore, the required probability is 0.24.