Answer:
The location of the new cell phone tower is
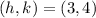 , and the equation of the circle is
, and the equation of the circle is
 .
.
Explanation:
The location of the cell phone tower coincides with the location of a circunference passing through the three cell phone towers. By Analytical Geometry, the equation of the circle is represented by the following general formula:
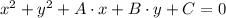 (1)
(1)
Where:
 - Independent variable.
- Independent variable.
 - Dependent variable.
- Dependent variable.
 ,
,
 ,
,
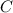 - Circunference constants.
- Circunference constants.
Given the number of variable, we need the location of three distinct points:
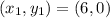
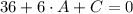


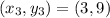
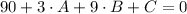
Then, we have the following system of linear equations:
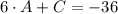 (2)
(2)
 (3)
(3)
 (4)
(4)
The solution of this system is:
 ,
,
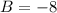 ,
,
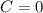
By comparing the general form with the standard form of the equation of the circunference is:
 (5)
(5)
 (6)
(6)
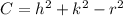 (7)
(7)
Where:
 ,
,
 - Coordinates of the center of the circle.
- Coordinates of the center of the circle.
 - Radius of the circle.
- Radius of the circle.
If we know that
 ,
,
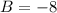 and
and
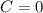 , then coordinates of the center of the circle and its radius are, respectively:
, then coordinates of the center of the circle and its radius are, respectively:

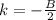
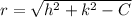
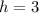 ,
,
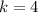 ,
,
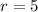
The location of the new cell phone tower is
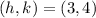 , and the equation of the circle is
, and the equation of the circle is
 .
.