Question

Prove :
sin²θ + cos²θ = 1


thankyou ~​

Answer 1

See below

Explanation:

Here we need to prove that ,

`\sf\longrightarrow sin^2\theta + cos^2\theta = 1`

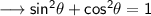
Imagine a right angled triangle with one of its acute angle as
`\theta` .

• The side opposite to this angle will be perpendicular .
• Also we know that ,

`\sf\longrightarrow sin\theta =(p)/(h) \\`

`\sf\longrightarrow cos\theta =(b)/(h)`

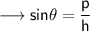
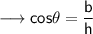
And by Pythagoras theorem ,

`\sf\longrightarrow h^2 = p^2+b^2 \dots (i)`

Where the symbols have their usual meaning.

Now , taking LHS ,

`\sf\longrightarrow sin^2\theta +cos^2\theta`

• Substituting the respective values,

`\sf\longrightarrow \bigg((p)/(h)\bigg)^2+\bigg((b)/(h)\bigg)^2\\`

`\sf\longrightarrow (p^2)/(h^2)+(b^2)/(h^2)\\`

`\sf\longrightarrow (p^2+b^2)/(h^2)`

• From equation (i) ,

`\sf\longrightarrow\cancel{ (h^2)/(h^2)}\\`

`\sf\longrightarrow \bf 1 = RHS`

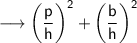
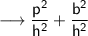
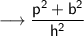
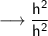
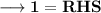
Since LHS = RHS ,

Hence Proved !

I hope this helps.