Question

A stack of paper contains 400 sheets. The volume of the stack is 140.25 cubic inches. Each sheet of paper is identical, with a length of 11 inches and a width of 8.5 inches. Find the height of each sheet of paper. Please put the process.

Answer 1

`0.00375\ \text{inches}`

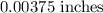
Explanation:

Volume of the stack of paper is 140.25 cubic inches

The length and width of the stack will be equal to that of a single sheet of paper so

`l=11\ \text{inches}`

`w=8.5\ \text{inches}`

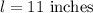
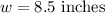
Let
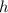`h` be the height of the stack.

Volume of the stack would be

`lwh=140.25\\\Rightarrow h=(140.25)/(lw)\\\Rightarrow h=(140.25)/(11* 8.5)\\\Rightarrow h=1.5\ \text{inches}`

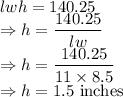
So the stack has a height of 1.5 inches. Now there are 400 sheet of paper in the stack.

Thickness of one sheet of paper is given by

`(1.5)/(400)=0.00375\ \text{inches}`

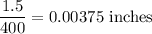
Hence, the height of each sheet of paper is
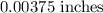`0.00375\ \text{inches}`.