Answer:
C
Explanation:
The volume of a box (rectangular prism) is given by:
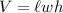
We are given that the desired volume is 540 cubic inches. The width is three inches longer than the length and the height is four inches longer than the length. Substitute:
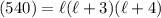
Solve for the length. Expand:

We cannot solve by grouping, so we can consider using the Rational Root Theorem. Our possible roots are:
±1, ±2, ±3, ±4, ±5, ±6, ±9, ±10, ±12, ±15, ±18, ±20, ±27, ±30, ±36, ±45, ±54, ±60, ±90, ±108, ±135, ±180, ±270, and/or ±540.
(If you are allowed a graphing calculator, this is not necessary.)
Testing values, we see that:
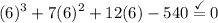
Hence, one factor is (x - 6).
By synthetic division (shown below), we can see that:
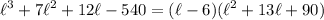
The second factor has no real solutions. Hence, our only solution is that l = 6.
In conclusion, our answer is C.