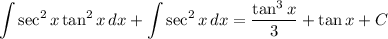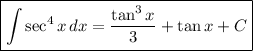Question

Help me with differentation and integration please!!

Answer 1

See below

Explanation:

`(d)/(dx) (\tan^3 x) = 3\sec^4 x - 3\sec^2 x`

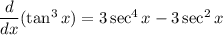
Recall

`(d)/(dx)\tan x=\sec^2`

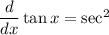
Using the chain rule

`(dy)/(dx)= (dy)/(du) (du)/(dx)`

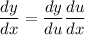
such that
`u = \tan x`

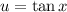
we can get a general formulation for

`y = \tan^n x`

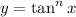
Considering the power rule

`\boxed{(d)/(dx) x^n = nx^(n-1)}`

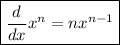
we have

`(dy)/(dx) =n u^(n-1) \sec^2 x \implies (dy)/(dx) =n \tan^(n-1) \sec^2 x`

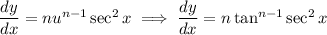
therefore,

`(d)/(dx)\tan^3 x=3\tan^2x \sec^2x`

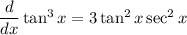
Now, once

`\sec^2 x - 1= \tan^2x`

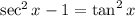
we have

`3\tan^2x \sec^2x = 3(\sec^2 x - 1) \sec^2x = 3\sec^4x-3\sec^2x`

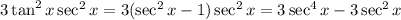
Hence, we showed

`(d)/(dx) (\tan^3 x) = 3\sec^4 x - 3\sec^2 x`

================================================

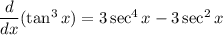
For the integration,

`$\int \sec^4 x\, dx $`

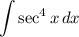
considering the previous part, we will use the identity

`\boxed{\sec^2 x - 1= \tan^2x}`

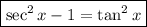
thus

`$\int\sec^4x\,dx=\int \sec^2 x(\tan^2x+1)\,dx = \int \sec^2 x \tan^2x+\sec^2 x\,dx$`

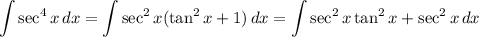
and

`$\int \sec^2 x \tan^2x+\sec^2 x\,dx = \int \sec^2 x \tan^2x\,dx + \int \sec^2 x\,dx $`

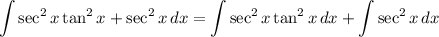
Considering
`u = \tan x`

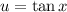
and then
`du=\sec^2x\ dx`

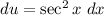
we have

`$\int u^2 \, du = (u^3)/(3)+C$`

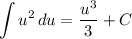
Therefore,

`$\int \sec^2 x \tan^2x\,dx + \int \sec^2 x\,dx = (\tan^3 x)/(3)+\tan x + C$`

`$\boxed{\int \sec^4 x\, dx = (\tan^3 x)/(3)+\tan x + C }$`