Question

Which of the following statements is not true? need help asap

Answer 1

B

Explanation:

a.Let prove each one.

`\sec(x) \tan(x) = \frac{ \sin(x) }{1 - \cos {}^(2) (x) }`

`(1)/( \cos(x) ) ( \sin(x) )/( \cos(x) ) =`

`\frac{ \sin(x) ) }{ \cos {}^(2) (x) }`

`\frac{ \sin(x) }{1 - \sin {}^(2) (x) }`

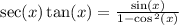
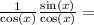
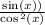
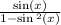
Since a is true, that isn't the answer.

b.

`\sec(x) + \cos(x) = \sin(x) \tan(x)`

`(1)/( \cos(x) ) + \cos(x) = \sin(x) \tan(x)`

`\frac{1 + \cos {}^(2) (x) }{ \cos(x) } ) = \sin(x) \tan(x)`

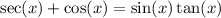
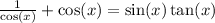
B doesn't seem right but for the sake of getting better, let see about c and d.

C.

`\csc(x) - \sin(x) = \cot(x) \cos(x)`

`(1)/( \sin(x) ) - \sin(x) = \cot(x) \cos(x)`

`\frac{1 - \sin {}^(2) ( x) }{ \sin (x) } = \cot(x) \cos(x)`

`\frac{ \cos {}^(2) (x) }{ \sin(x) } = \cot(x) \cos(x)`

`( \cos(x) \cos(x) )/( \sin(x) ) = \cot(x) \cos(x)`

`( \cos(x) )/( \sin(x) ) * \cos(x) = \cot(x) \cos(x)`

`\cot(x) \cos(x) = \cot(x) \cos(x)`

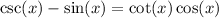
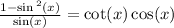
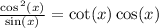
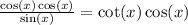
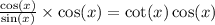
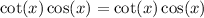
So c is right, so it isn't the answer.

`\frac{1 - 2 \sin {}^(2) (x) }{ \sin(x) \cos(x) } = \cot(x) - \tan(x)`

`\frac{ \sin {}^(2) (x) + \cos {}^(2) (x) - 2 \sin {}^(2) (x) }{ \sin(x) \cos(x) } = \cot(x) - \tan(x)`

`\frac{ \cos {}^(2) (x) - \sin {}^(2) (?) }{ \sin(x) \cos(x) } = \cot(x) - \tan(x)`

`\frac{ \cos {}^(2) (x) }{ \cos(x) \sin(x) } - \frac{ \sin {}^(2) x }{ \cos(x) \sin(x) }`

`( \cos(x) )/( \sin(x) ) - ( \sin(x) )/( \cos(x) ) = \cot(x) - \tan(x)`

`\cot(x) - \tan(x) = \cot(x) - \tan(x)`

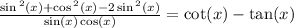
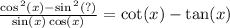
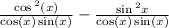
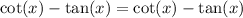
So D is right, So that isn't isn't answer.

It seems that B is the right answer since it isnt isn't true identity.