Question

A radio station tower was built in two sections. From a point that is 70 feet from the base of the tower, the angle of elevation to the top of the section is 28 degrees, and the angle of elevation to the top of the second section is 40 degrees. What is the height of the top section of the tower to the nearest tenth of a foot?

Answer 1

21.5 feet

Explanation:

d = Distance of the bottom of the tower to the point of observation

x = Height of the top section of the tower

a = Height of bottom section

b = Total height of tower

`\tan28^(\circ)=(a)/(d)\\\Rightarrow a=d\tan28^(\circ)\\\Rightarrow a=70\tan28^(\circ)`

`\tan40^(\circ)=(b)/(d)\\\Rightarrow b=d\tan40^(\circ)\\\Rightarrow b=70\tan40^(\circ)`

`x=b-a\\\Rightarrow x=70\tan40^(\circ)-70\tan28^(\circ)\\\Rightarrow x=70(\tan40^(\circ)-\tan28^(\circ))\\\Rightarrow x=21.5\ \text{feet}`

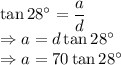
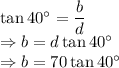
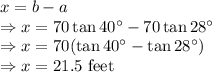
The height of the top section of the tower is 21.5 feet.