Question

PLEASE HELP: write a possible function, f(x), in factored form that could model the graph below​

Answer 1

Hi there! Your answer is f(x) = x(x+3)²(x-4)

Please see an explanation for a clear and better understanding to your problem.

Any questions about my answer or explanation can be asked through comments! :)

Explanation:

This type of graph is called Graph of Polynomial Function. They have a degree of n where n is the positive integer. The polynomial functions can be broken into these two categorizes:

• Odd-Degree
• Even-Degree

Note that they are for graph purpose only, may not appear in curriculum.

Odd-Degree functions will have graphs that start from negative infinity to positive infinity for f(x) term. Please see first and two attachments for a clear understanding.

Even-Degree functions will have graphs that start from positive infinity to positive infinity for f(x) term. Please see third and fourth attachment.

Therefore, the graph is even-degree polynomial because it starts from positive infinity where f(x) is decreasing to positive infinity where f(x) is increasing.

Next is to find a factored from of function. Factored forms are basically x-intercepts form of function. Please see the formula.

`\large\boxed{f(x)=(x-a)(x-b)(x-c)}`

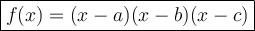
This is an example of factored form. The x-intercepts are at a, b and c. Just like how you solve an equation.

So what we need to do is to find x-intercepts.

The graph has x-intercepts at these following:

• x = -3 (Double)
• x = 0
• x = 4

Then we convert them into factored form including swapping from positive to negative and negative to positive. We should get:

`\large{f(x)=(x+3)^2(x+0)(x-4)}\\\large{f(x)=x(x+3)^2(x-4)}`

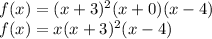
Notice if we multiply these, we'd get 4-degree polynomial.

[ Reference to double of x = -3 ]

The graph suddenly shifts up when f(x) = 0 on x = -3. Hence, implying that x = -3 are doubled also known as (x+3)(x+3) = (x+3)²