Question

7.) The mean rate for a satellite television from a sample of households was $51.00 per month,

with a standard deviation of $2.00 per month. Between what two values do 75% of the data lie?
(Assume a bell-shaped distribution.) (HINT: Chebychev's Theorem)

Answer 1

Answer: 75% of the rate lies in 47 per month and 55 per month.

Explanation:

The mean rate for a satellite television from a sample of households was $51.00 per month, with a standard deviation of $2.00 per month.

According to the Chebychev's Theorem, atleast
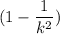`(1-(1)/(k^2))` % of the data lies within k standard deviation from the mean.

For k=2

`1-\frac1{2^2}=1-\frac14=\frac34=0.75\ or \ 75\%`

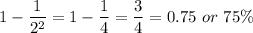
Alteast 75% of data lies within 2 standard deviation from mean.

i.e. 51-2(2) per month and 51+2(2) per month

i.e. 47 per month and 55 per month

Hence, 75% of the rate lies in 47 per month and 55 per month.