9514 1404 393
Answer:
"complete the square" to put in vertex form
Explanation:
It may be helpful to consider the square of a binomial:
(x +a)² = x² +2ax +a²
The expression x² +x +1 is in the standard form of the expression on the right above. Comparing the coefficients of x, we see ...
2a = 1
a = 1/2
That means we can write ...
(x +1/2)² = x² +x +1/4
But we need x² +x +1, so we need to add 3/4 to the binomial square in order to make the expressions equal:
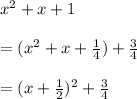
_____
Another way to consider this is ...
x² +bx +c
= x² +2(b/2)x +(b/2)² +c -(b/2)² . . . . . . rewrite bx, add and subtract (b/2)²*
= (x +b/2)² +(c -(b/2)²)
for b=1, c=1, this becomes ...
x² +x +1 = (x +1/2)² +(1 -(1/2)²)
= (x +1/2)² +3/4
_____
* This process, "rewrite bx, add and subtract (b/2)²," is called "completing the square"—especially when written as (x-h)² +k, a parabola with vertex (h, k).